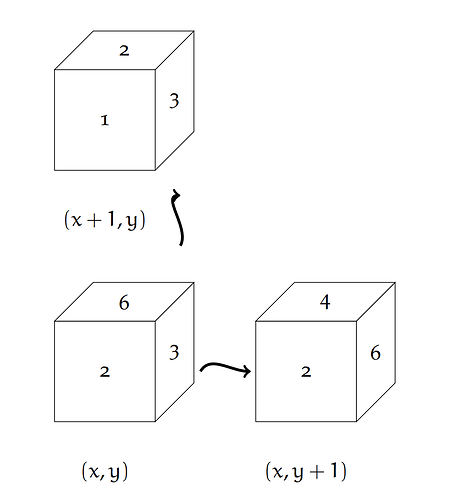Are cineva idee cum as putea rezolva aceasta problema in Java sau C++?
Enunt:
Se da un grid de N x M si un zar cu costuri pe fiecare dintre cele 6 fete. Initial,
zarul se afla pe pozitia (Sx, Sy) din grid, asezat ca in figura de mai jos, cu fata
numerotata cu 1 in contact cu casuta de start a gridului. Putem sa mutam zarul in
oricare dintre cele 4 directii (sus, jos, stanga, dreapta), iar o mutare consta in
rostogolirea zarului in directia corespunzatoare.
Stiind ca exista casute blocate in matrice, se cere costul minim de a deplasa zarul
din pozitia (Sx, Sy) in pozitia (Fx, Fy).
Costul deplasarii zarului intre 2 pozitii date este dat de suma costurilor fetelor
pe care este asezat zarul pe parcursul deplasarii.
Date de intrare:
Pe prima linie a fisierului rtd.in se afla 7 numere intregi, N, M, Sx, Sy, Fx, Fy,
K, reprezentand dimensiunile gridului, pozitia de start si pozitia de final a zarului,
respectiv numarul de casute blocate din matrice.
Pe a doua linie se afla 6 numere intregi, al i-lea numar fiind egal cu costul de pe
a i-a fata.
Pe urmatoarele K linii se afla cate 2 numere intregi X si Y, cu semnificatia ca
pozitia (X, Y) este blocata.
Date de iesire:
Fisierul rtd.out va contine un singur numar, egal cu costul minim de deplasare
intre cele 2 pozitii date.
Restrictii si precizari:
• Suma indicilor fetelor opuse este mereu 7.
• Se garanteaza ca pozitiile (Sx, Sy) si (Fx, Fy) nu sunt blocate.